Can RuleFit Improve The Fama French 3 Factor Model?

Image Credit: Patiwat Sariya / Shutterstock.com
Statistical models are a lot like cooking methods. When you’re cooking, you can use the same ingredients to make a wide variety of meals. For instance, you can turn the same potato into fries or mashed potatoes.
Different statistical models likewise have the ability to use the same data but output different results. One model may examine Apple’s price history and predict that its stock will go up tomorrow. Another may reach the exact opposite conclusion. But unlike cooking, we can usually conclude that one model is superior to another for a given data set, because there are objective ways to evaluate the results.
My interest therefore perked up when I read about a new statistical model called RuleFit, from Christoph Molnar’s terrific book, “Interpretable Machine Learning”. What’s interesting about RuleFit is that it extends linear regressions to incorporate interactions among independent variables.
One of the biggest drawbacks of linear regression is that it can’t model interactions between factors very well. To explain, let’s use the example of snacks.
There are many delicious snacks that are sweet, and many that are salty. Now, suppose you want to model deliciousness using a linear regression, where we use sweetness and saltiness as factors. Then, I’d imagine the model would say that increasing sweetness would make the snack more delicious, and so would increasing saltiness. Those conclusions would sound reasonable in isolation.
However, the model would also say that the most delicious snacks would be those that are both sweet and salty, which wouldn’t sound quite right. Sweetness and saltiness would conflict with each other, leading to a poorer outcome than if the snack was purely sweet or purely salty. Linear regressions don’t have that ability to consider such conflicts.
To incorporate factor interactions (such as the sweetness vs. saltiness conflict), we generally have to use more complex statistical models. But unfortunately, using these more complex models often comes at a cost. Whereas linear regression models are very easy to interpret, most of the more complex models are not. Would increasing sweetness make a snack tastier? You’d no longer be sure by just looking at the configuration of the model.
And that’s where RuleFit comes in.
RuleFit consists of two parts. The first part is the same as a linear regression. If we’re trying to model the deliciousness of a snack, we’d have the sweetness, saltiness and their coefficients in there. The second part consists of rules and their coefficients. For example, let’s say that there’s a rule that says [(sweetness is above average) and (saltiness is above average)], and the coefficient of this rule is negative. Such a model would penalize the taste score in situations where sweetness and saltiness are above average.
Having discovered RuleFit, I was curious to see if using it would yield any new insights in finance. I therefore decided to try it on the famous Fama French 3 factor model (FF3).
In case you’re not aware, the FF3 model is a linear regression involving broad market returns, size premium and value premium as factors to explain stock price movements. I’ve long wondered if accounting for interactions among the three factors would improve the model. I therefore decided to use the same factors as the FF3 model, but use RuleFit instead.
To run my experiment, I used historical factors data from AQR’s website, and individual stock price data from S&P’s Xpressfeed database. I then fit 50 randomly chosen NYSE or NASDAQ listed stocks for analysis. Some of you may wonder if 50 stocks is enough for my analysis, and I believe it is. I’ve run the code a few times, and the results seem to be consistent.
For each stock, I fit both linear regression and RuleFit models using historical data from 2000 to 2014. I used the linear regression model included in the scikit-learn library, and the RuleFit model provided by Christoph Monar. There were a few different hyperparameters that I could tune for the RuleFit model, but I decided to tune only one of them: the maximum number of rules. By default, the RuleFit library would have created up to 2000 rules, which I felt would lead to overfitting. To begin with, I set the maximum number of rules to 100.
I then made predictions using both models for the 2015-2019 period, and obtained their respective R-squared metrics to judge how well they explained stock price returns.
Unfortunately, RuleFit didn’t appear to have improved on linear regression at all. While linear regression models averaged R-squared of 13.5%, RuleFit models’ R-squared actually came in worse, at 12.7%. The difference between these numbers is small enough, however, that it’s probably statistically insignificant. The average absolute difference between the two R-squareds was 1.9% per stock.
The following graph shows the sample plot of predictions generated by the two models. The x axis shows the actual stock price returns, and the y axis shows the predictions.
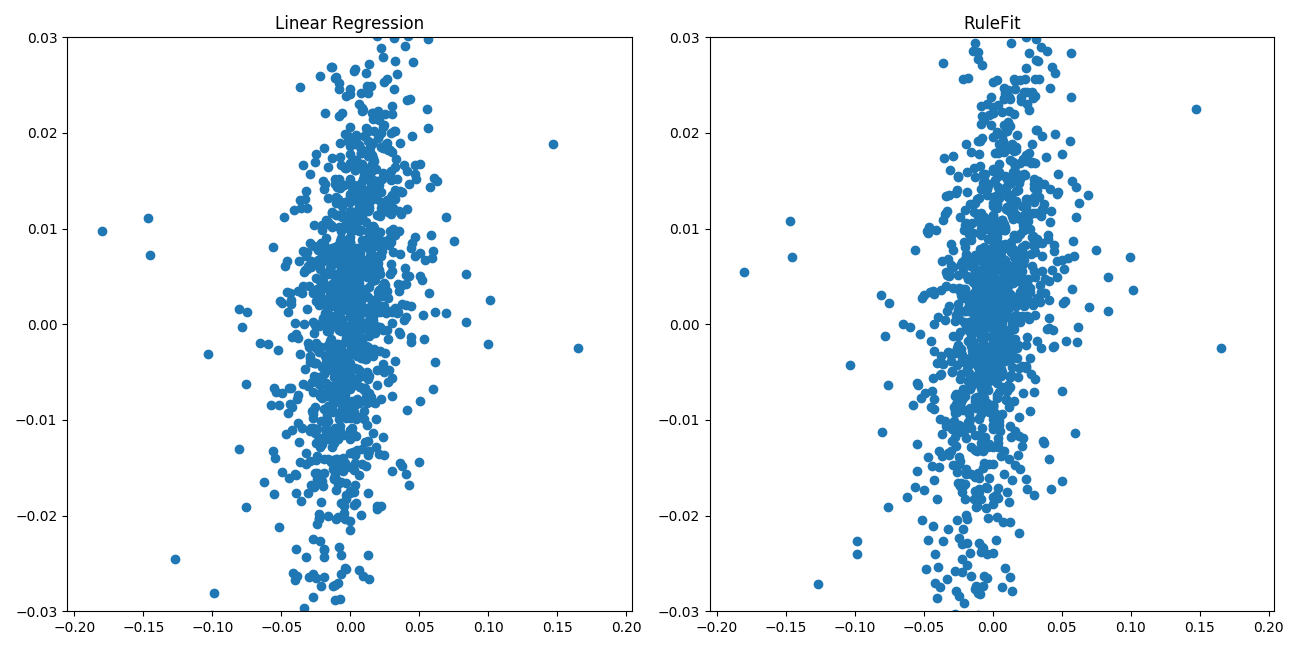
We can see that the graphs look similar, suggesting that the rules part generally didn’t play a major role in determining the predictions. But whatever role the rules played, it didn’t help generate better predictions.
I wondered if RuleFit wasn’t generating good results because of the high maximum number of rules. With 100 rules, that meant RuleFit models had 3 coefficients for the linear regression factors, and 100 coefficients for the various rules. I therefore tried running RuleFit with a maximum of 10 rules, but the results were essentially the same. The RuleFit R-squareds were slightly worse, and the prediction charts looked very similar to that of linear regression models.
So why couldn’t RuleFit improve on linear regression? One potential reason is that there is nothing to gain from modelling interactions between the different factors, at least for the FF3 model. However, I’m skeptical that this is the case, since there are some fairly significant correlations between the different factors. I admit though that this is a gut feeling, rather than a scientifically rigorous conclusion.
The other potential reason may be that RuleFit is a poor choice for modelling factor interactions. This seems to be the likelier explanation, given that it agrees with Christoph Molnar’s experience. In his book, “Interpretable Machine Learning”, Molnar stated that he had tried RuleFit a few times, but the results were “disappointing”.
In conclusion, I really liked the promise of RuleFit as a way of improving on linear regression without losing its inherent interpretability. Unfortunately, I’ve found the performance of the model has been disappointing, at least when used in the context of modeling stock prices using the Fama and French 3 factors.



